Сказки

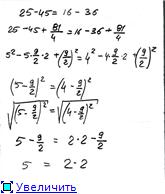     Сегодня мы продолжим решать примеры с арифметическим корнем задание № 3 ГИА по математике. Из вчерашних примеров можно было заметить, что не всегда есть необходимость решать примеры до конца. Есть варианты приближённого вычисления, и сегодня мы их рассмотрим:

1.  Между какими целыми числами расположено число -√13 + 1
Обратим внимание, что 13 находится между квадратами 3 и 4, соответственно между 9 и 16. Значит, принимаем √13 примерно 3,5. Со знаком минус, или -3,5 + 1  ≈ -2,5.  Данное число располагается между целыми -3 и -2.

2. Между какими целыми числами расположено значение выражения  (-√5 – 3)² – 1
Раскрываем скобки и возводим выражение в квадрат. Имеем:
5 + 2·3·√5 + 9 – 1 = 6√5 + 13. Теперь это выражение можно решать так,  как мы делали это вчера:
a+12<6√5 + 13<а + 13  или   6√5 + 13<а + 13, т.е. а>√180, или а²>180 = 169+11 = 13² + 11. Получается, что а>13. Ближайшее целое к а число равно 14.  Но нас интересует а+12 и а+13, т.е. 14+12 и 14+13. Или 26 и 27.
У нас получился ответ: выражение  (-√5 – 3)² – 1 расположено между целыми числами 26 и 27.

3. Найти значение выражения  1/√27 + 1/√3
1/√27 + 1/√3 = (√3 + √27)/√27·√3 = (√3 + 3·√3)/√81 = 4·√3/9

4. Найти значение выражения  √0,48 · 1/√12
√0,48 · 1/√12 = √0,48/√12 = √(0,48/12) = √0,04 = 0,2

5.  Найдите значение выражения 3/5  · √75 =  3·√75/5 = 3·√25·3/5 = 3·5·√3/5  = 3·√3

6. Расположить в порядке возрастания: 4√21     4√5   9
4√21 = √16·21 = √336
4√5 = √16·5 = √80
9 = √81      Итак, мы располагаем числа в порядке возрастания:    4√5      9    4√217.

7. Расположить в порядке убывания:  6      4√3         (√5 – 1)²
Рассматриваем  6 и 4√3 :           6=√36        4√3= √16·3 = √48
Разбираем  (√5 – 1)²   Корень из 5 чуть больше 1,4, да ещё – 1, получаем ≈0,4,  да в квадрате  ≈ 0,16 – самое маленькое.
Отсюда имеем расположение в порядке убывания:    4√3       6         (√5 – 1)² 

8. Расположить в порядке возрастания:   10,   3√10,    √88
10 = √100           3√10 = √9·10 = √90        √88.      Располагаем в порядке возрастания √88,     3√10,       10

9. Расположить в порядке убывания:    2-√5,       – 19/7         (-√7 – 1)²
Третье выражение положительно.
Первое отрицательно, т.к. √5 ≈ 2,2, имеем 2-2,2 = -0,2
Второе тоже отрицательно ≈ – 2,7.   Отсюда имеем в порядке убывания     (-√7 – 1)²,     2-√5,       – 19/7  

10. Расположить в порядке возрастания: 2√3 – √12,       -√7,       1 – √3
Первое  выражение    2√3 – √12 = 2√3 –  √2²·3 =  2√3 –  2√3 = 0
Второе число примерно – 2,7
Третье  1 – ≈1,7  ≈ – 0,7.  Итого в порядке возрастания:    -√7,       1 – √3,     2√3 – √12

На сегодня мы закончим решать примеры с арифметическим корнем из задания № 2 по математике ГИА. До новых встреч и успехов!