Сказки

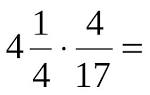      Задание  1 по математике ГИА так или иначе связано с дробями. Десятичными, простыми, смешанными дробями, а также с  арифметическими действиями с ними.
Решая это задание необходимо знать и помнить несколько основных правил:
       1.Если числитель и знаменатель дроби  умножить или разделить одновременно на одно и то же число, отличное от  нуля, то значение дроби останется прежним.
       2.Для сложения и вычитания дробей с разными знаменателями их необходимо привести к общему знаменателю. Для этого нам поможет НОК (наименьшее общее кратное) – наименьшее число, которое делится на каждое из данных чисел.
      3.При умножении простых дробей перемножают соответственно числители и знаменатели этих дробей.
       4.Чтобы умножить дробь на число, необходимо числитель дроби умножить на это число, а знаменатель оставить без изменения.
       5.Вводим понятие обратной дроби.  Обратная дробь – это дробь, у которой числитель и знаменатель поменяли местами.  Для того, чтобы найти обратную дробь к смешанной дроби, надо сначала смешанную дробь превратить в неправильную, а затем поменять местами числитель и знаменатель. Произведение прямой и обратной дроби всегда дают в итоге 1.    Чтобы разделить одну обыкновенную дробь на другую надо вторую дробь представить в виде обратной и произвести умножение.
       6.Десятичная дробь – специальная форма записи дроби, в знаменателе которой стоят 10, 100, 1000 и т.д. Прежде, чем делить число на десятичную дробь, надо умножить делимое и делитель на 10, 100, 1000 и т.д. так, чтобы делитель стал целым числом. При этом запятые передвинутся вправо на одинаковой количество цифр. А если цифр не хватает, припишем нули.

Итак, примеры:

1.  0,7·3,6/0,9 = 7·36/90 = 7·4·9/9·10 = 7·4/10 = 28/10 = 2,8

2. 0,6·1,4/2,1 = 6·14/210 = 2·3·2·7/7·2·3·5 = 2/5 = 2·2/5·2 = 4/10 = 0,4

3. 0,7·2,2/2,8 = 7·22/280 = 7·2·11/7·2·20 = 11/20 = 11·5/20·5 = 55/100 = 0,55

4. 0,2·3,3/1,2 = 2·33/120 = 2·3·11/2·3·20 = 11/20 = 0,55

5. 2,1·1,1/0,4·1,5 =  21·11/4·15 = 3·7·11/4·3·5 = 77/20 = 77·5/20·5 = 385/100 = 3,85

6. 2,2·2,1/0,15·11 = 22·21/15·11 = 2·11·3·7/3·5·11 = 14/5 = 14·2/5·2 = 28/10 = 2,8

7. 0,6·2,8/0,4 = 6·28/40 = 2·3·4·7/4·10 = 42/10 = 4,2

8. 0,7·3,5/0,5 =  7·35/50 = 7·7·5/5·10 = 49/10 = 4,9

9. (3/4 – 1)²·8 +5 = (-1/4)²·8 + 5 = (1/16)·8 + 5 = 1/2 + 5 = 5,5

10. (16/3 + 1)·6 + (1/2)² = (19/3)·6 + 1/4 = 19·2·3/3 + 25/100 = 38 + 25/100 = 38,25

11. 5,2·(2/13) + (-1/2)³ = (26/5)·(2/13) + (-1/8) = 13·2·2/·5·13 – 125/1000 = 4/5  – 0,125 = 0,8 – 0,125 = 0,675

12. (7/15)·4,5 – (-1/5)² = (7/15) ·(45/10) – (1/25) = 7·3·15/15·10 – 0,04 = 21/10 – 0,04 = 2,1 – 0,04 = 2,06

На сегодня всё. В следующий раз мы продолжим решение примеров из ГИА математики  задание  1.