Сказки

Начинаем второй  урок, посвящённый изучению теорем, аксиом и определений, геометрии 7 класса.

25.    СВОЙСТВО ПЕРПЕНДИКУЛЯРА К ПРЯМОЙ – это достаточно сложное определение, в котором будет 4 раза слово «дано, данный», и ни одного из них пропустить нельзя. Читаем: ИЗ   ДАННОЙ   ТОЧКИ, КОТОРАЯ ЛЕЖИТ НА   ДАННОЙ  ПРЯМОЙ  К   ДАННОЙ  ПРЯМОЙ   В   ДАННОЙ  ПОЛУПЛОСКОСТИ МОЖНО ВОССТАВИТЬ ТОЛЬКО ОДИН ПЕРПЕНДИКУЛЯР.

26.       Биссектриса – полупрямая, которая исходит из вершины угла и делит угол пополам.

 

 

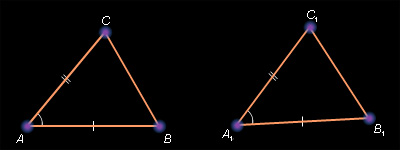27.       Признаки равенства треугольников. Следствие.
– если две стороны и угол, заключённый между ними одного треугольника, соответственно равны двум сторонам и углу заключенному между ними, другого треугольника, то такие треугольники равны;
– если сторона и два прилежащих к ней угла одного треугольника, соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны;
– если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
СЛЕДСТВИЕ.  В равных треугольниках против равных сторон лежат равные углы и против равных углов лежат равные стороны.

 

28.       Медиана – это отрезок, который соединяет вершину треугольника с серединой  противоположной стороны.

 

 

 

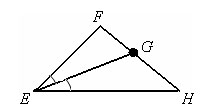29.       Биссектриса треугольника  – это отрезок биссектрисы угла треугольника, заключенный между вершиной и противоположной стороной. У биссектрисы угла есть начало, но нет конца, а у биссектрисы треугольника есть начало и есть конец.

 

 

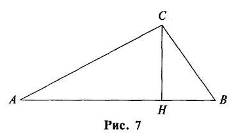30.       ВЫСОТА – 2 определения, по Атанасяну и Погорелову:
– высота треугольника – это перпендикуляр, опущенный из вершины треугольника на
противоположную сторону или её продолжение;
– это перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.

 

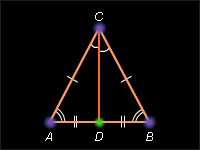31.       Равнобедренный треугольник и его свойства:
– равнобедренный треугольник – это треугольник, у которого две стороны равны.
Свойство – в равнобедренном треугольнике углы при основании равны.

32.       Свойство медианы равнобедренного треугольника:
– медиана угла при вершине равнобедренного треугольника является одновременно биссектрисой и высотой.

33.      Свойство двух прямых, параллельных третьей:
– если две прямые ПОРОЗНЬ  параллельны одной и той же третьей, то они параллельны между собой.

34.        Углы при параллельных и секущей:
– при пересечении двух прямых третьей образуется 4 пары односторонних углов, 4 пары накрест лежащих углов и 4 пары соответственных углов.

35.        Признаки параллельности прямых:
– если при пересечении двух прямых третьей окажется, что какие-нибудь накрест лежащие углы равны, или какие-нибудь соответственные углы равны, или какие-нибудь односторонние в сумме дают 180 градусов, то такие прямые параллельны.

36.        Свойство накрест лежащих, соответственных и односторонних углов:
– если две параллельные прямые пересечены третьей, то накрест лежащие углы равны, соответственные углы равны и односторонние углы в сумме равны 180°.

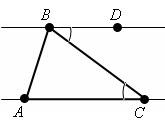37.       Сумма углов треугольника – равна 180°.
Следствия:
- в равностороннем треугольнике все углы равны 60°;
- в прямоугольном треугольнике сумма острых углов равна 90°;
- в прямоугольном равнобедренном треугольнике острые углы равны по 45°;
- в прямоугольном треугольнике катет, лежащий против угла 30°, равен половине
гипотенузы;
- внешний угол треугольника равен сумме двух внутренних углов, не смежных  с ним:
- если два угла одного треугольника равны двум углам другого треугольника, то и третьи углы у них равны.

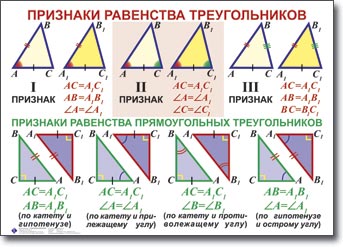38.      Признаки равенства прямоугольных треугольников:
1. если катеты одного треугольника соответственно равны катетам другого треугольника, то такие треугольники равны;
2. если катет и прилежащий к нему острый угол одного треугольника соответственно  равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны;
3. если катет и противолежащий  к нему острый угол одного треугольника соответственно  равны катету и противолежащему  к нему острому углу другого треугольника, то такие треугольники равны;
4. если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны;
5. если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

39.      Теорема о единственности опущенного перпендикуляра:
– из точки вне прямой на прямую можно опустить перпендикуляр и притом только один.

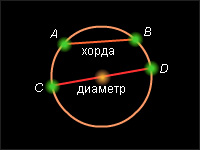40.     Окружность, круг, хорда, диаметр, радиус, дуга, сектор, сегмент:
– окружность – кривая, замкнутая на плоскости, все точки которой одинаково удалены от центра окружности;
– круг – часть плоскости, ограниченная окружностью;
– хорда – отрезок, который соединяет две точки окружности;
– диаметр – хорда, проходящая через центр окружности;
– радиус – отрезок, соединяющий центр с точкой на окружности;
– дуга – часть окружности;
– сектор – часть круга, заключённая  между двумя радиусами и дугой;
- сегмент – часть круга, заключённая между хордой и дугой.

41.     Геометрическое место точек (ГМТ) – все точки плоскости или пространства,
которые имеют одни и те же свойства.

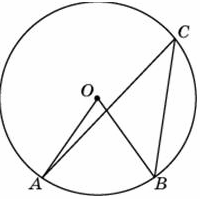42.    Центральный угол – угол, вершина которого  в центре окружности, а стороны
пересекают окружность.

43.    Вписанный угол и его измерение.
– вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность;
– вписанный угол измеряется половиной дуги, на которую он опирается;
– вписанный угол равен половине центрального, стороны которого проходят через те же точки окружности, что и стороны вписанного угла, а если вписанный угол тупой, то он дополняет половину центрального до 180°.
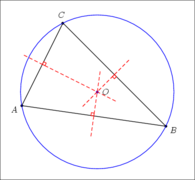44.    Первая замечательная точка треугольника:
– три срединных перпендикуляра пересекаются в одной точке, и эта точка является центром описанной окружности.

 

 

 

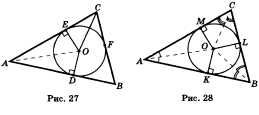45.    Вторая замечательная точка треугольника:
– три биссектрисы углов треугольника пересекаются в одной точке, и эта точка
является центром вписанной окружности.
1 урок    3 урок