Сказки

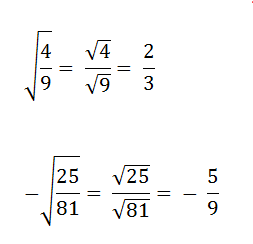Как и три предыдущих дня, сегодня мы будем решать примеры задания № 3 ГИА на тему математика квадратного корня.

1. Известно, что х=2+√3, у=2-√3.  Необходимо указать, какое из следующих чисел иррационально.
х+у       х-у        ху         х-√3
Мы видим, что х представляет собой сумму двух чисел: 2 и √3, а у – их разность.
Значит, в сумме они дадут удвоенное первое число: 2+√3 + 2-√3 = 4.
Произведение ху дает нам разность квадратов: (2+√3)(2-√3) = 2² – (√3)² = 4-3 = 1.
Поскольку  х=2+√3, то разность между х  и √3 даёт нам 2.
Остаётся последнее число х – у = 2+√3 – (2-√3) = 2 + √3 – 2 + √3 = 2√3.
Это и будет иррациональное число. 

2. Известно, что х=√5 – 1,  у=√5 + 1.  Необходимо указать, какое из следующих чисел иррационально.
х+у       у+√5        ху         х-√5
Как и в первом случае х – разность двух чисел √5  и 1, а у – сумма.
Произведение этих чисел будут равно:  (√5 – 1)(√5 + 1) = (√5)² – 1 = 5 – 1 = 4
Разность  между ними будет √5 – 1 – (√5 + 1) = √5 – 1 – √5 – 1  = -2
х-√5 = √5 – 1 – √5 = -1
Остаётся  у+√5 = √5 + 1 + √5 = 2√5 + 1. Это и есть иррациональное число.

3. Значение какого из выражений является числом иррациональным?
√2·√32      √64/√25        (4 – √7)(4 +√7)           (√5 – 8)²
Первое выражение представляет собой произведение двух одинаковых корней.
Значит, согласно п. 4, их можно объединить под один знак. Имеем √2·√32 = √64 = 8.
Второе выражение вычисляется легко:  √64/√25 = 8/5 = 1,6
Третье представляет собой разность квадратов двух чисел  (4 – √7)(4 +√7) = 4² – (√7)² = 16 – 7 = 9.
Остаётся четвёртое – квадрат разности двух чисел: (√5 – 8)². Оно и является иррациональным, поскольку при разложении мы имеем удвоенное произведение первого числа на второе: 2·8·√5 = 16√5.

4. Значение какого из выражений является числом иррациональным?
(7 – √5)(7 +√5)                 (√5)²/√49              (7 -√3)²           √5·√45
Третье выражение, являющееся квадратом разности двух чисел
(7 -√3)²,  имеет  в себе удвоенное произведение первого числа на второе, а именно: 2·7·√3 = 14√3.
Оно и будет иррациональным. Остальные выражения  рациональны. Читатель может проверить это сам.

5. Значение какого из выражений является числом рациональным?
(2 – 5√5)(2 +5√5)    √7/(√5)²   (9 -3√7)²  √5·√13
Если рассматривать предыдущие варианты (п.п. 3 и 4), то можно заметить, что первое выражение – разность квадратов двух чисел и является рациональным числом:
(2 – 5√5)(2 +5√5) = 2²  – (5√5)²  = 4 – 25·5 = 4 – 125 = – 121.
Проверим остальные выражения: во втором в числителе корень из 7,
в знаменателе число 5 – иррациональное.
Третье выражение – квадрат разности двух чисел имеет в себе удвоенное произведение  первого числа на второе,
а именно 2·9·3√7 =  54√7  – иррациональное число.
И последнее выражение при объединении корня имеет подкоренное выражение 65.
Тоже иррациональное число.

6. Значение какого из выражений является числом рациональным?
(6 – 2√7)(6 +2√7)        (√13)²/√17      (2√3 – 5)²     √11·√3
Опять здесь присутствует разность квадратов в первом выражении.
(6 – 2√7)(6 +2√7)  = 36 – 4·7 = 36 – 28 = 8.
Остальные выражения  иррациональны. См п.п 3-5.

7. Расставить по убыванию числа:
7,        9 – √5,        √37 + 1
Отнимем от первого числа второе, получим:
7 – (9 – √5) = 7 – 9 +√5 = √5 – 2 = √(4+1) – 2 = √(2²+1) – 2.
Под корнем число больше 2, вычитаем 2 получается положительное число.
Значит   7  > 9 – √5,
Теперь вычтем из первого числа третье:
7  – (√37 + 1)  = 7  – √37 – 1 = 6 – √37 =6 – √(36+1) = 6 – √(6²+1).
Под корнем число больше 6, значит, третье число больше первого.
Имеем по убыванию: третье, первое, второе.

8. Расставить по возрастанию числа:
8 – √2,       √21 + 1,         6
Так же, как и в предыдущем варианте. Отнимем от первого числа  третье.
8 – √2 – 6 = 2 – √2.  Квадрат числа, большего 1, всегда больше самого числа.
Значит, 2 – √2 – положительно. Первое больше третьего.
Теперь сравним второе и третье.
√21 + 1 –  6  =  √21 – 5 =√(25 – 4) – 5 = √(5² – 4)  – 5.
Подкоренное выражение меньше 5². Значит корень из √(5² – 4)<5.
Т.е. второе число меньше, чем третье.   Имеем по возрастанию: второе, третье, первое.

9. Значение какого из выражений является числом рациональным?
(2√5-3)(2√5+3)           (√14)²/√6             (4-√2)²           √7·√9
И опять в первом выражении можно увидеть разность квадратов.
Имеем: (2√5-3)(2√5+3)= 4·5 – 9 = 20-9=13.
Остальные выражения иррациональные, в чём уважаемый читатель может убедиться сам.

10.  Значение какого из выражений является числом рациональным?
(√5+√17)²,     √8·√9,    √125/3·√5,       (√5+√7)/(√5-√7)
Первое выражение – квадрат суммы двух чисел.
Оно имеет в себе удвоенное произведение первого числа на второе,
а именно: 2·√5·√17 = 2√85 – иррациональное число.
Второе выражение преобразуем в следующее:
√8·√9 = √8·9 = √2²·2·3² =  2·3√2 = 6√2 – иррациональное число.
Третье выражение имеет следующее решение:
√125/3·√5 = (√125/5)·(1/3) = √25/3 = 5/3 – рациональное число.
Проверим четвёртое выражение:
(√5+√7)/(√5-√7) = (√5+√7)²/(√5-√7)(√5+√7) =  (√5+√7)²/(5-7) = – (√5+√7)²/2.
В числителе квадрат суммы, в знаменателе – рациональное число,
значит вся дробь – иррациональна.
Ответ: третье выражение рационально.

Мы закончили очередной день решением примеров на тему математика  квадратного корня. На следующей неделе мы продолжим  решение вариантов ГИА задания № 3. До новых встреч и успехов!